type
status
date
slug
summary
tags
category
icon
password
文章目录
- * 第3章 数据结构与算法
- * 3.1 线性结构
- * 3.1.1 线性表
- 3.1.2 栈和队列
- 3.1.3 串
- 3.2 数组和矩阵 87
- 3.3 树和图 90
- * 3.3.1 树 90
- 3.3.2 图 97
- 3.4 常用算法 102
- * 3.4.1 算法概述 102
- 3.4.2 排序 105
- 3.4.3 查找 112
- 3.4.4 递归算法 122
- 3.4.5 图的相关算法 123
第3章 数据结构与算法
3.1 线性结构
- **线性表的定义**
一个线性表是n个元素的有限序列(n≥0),通常表示为(a1,a2, a3,……,an)。
- **线性表的存储结构**
(1) **顺序存储**
用一组地址连续的存储单元依次存储线性表中的数据元素,从而使得逻辑关系相邻的两个元素在物理位置上也相邻。
优点:可以随机存取表中的元素
缺点:插入和删除操作需要移动大量的元素

(2) **链式存储**
用节点来存储数据元素,元素的节点地址可以是连续的,也可以是不连续的。
优点:插入和删除操作不需要移动元素
缺点:不能进行数据元素的随机访问

单链表:
不能随机访问表中的任一结点,必须从头结点依次.next。
循环链表:

双向链表:

(1) **顺序查找**
算法非常简单,但是效率较低,因为它是用所给关键字与线性表中各元素的关键字逐个比较,直到成功或失败。
(2) **折半查找**
优点是比较次数少,查找速度快,平均性能好;
缺点是要求待查表是有序表,且插入和删除困难。
适用于不经常变动而查找频繁的有序列表。
一般不进行表的插入和删除操作。
需要对中间元素进行快速定位,在链表结构上无法实现。
(3) **分块查找**
又称索引查找,主要用于分块有序表的查找。所谓分块有序是指将线性表 L (一堆数组)分成m个子表(要求每个子表的长度相等),且第 i+1
个子表中的每一个项目均大于第 i 个子表中的所有项目。因此,分块查找的关键在于建立索引表,其查找的平均长度介于顺序查找和折半查找之间。
- **栈** (21年第5题)
栈是按“后进先出”的规则进行操作的。
(1)**顺序栈**
用一组地址连续的存储单元依次存储自栈顶到栈底的数据元素。
存储空间是预先定义或申请的,因此可能会出现栈满的情况。每一个元素入栈时都要判断栈是否已满。需要设置一个头指针指到栈顶。需要附设指针 top
指示栈顶元素的位置
(2)**链栈**
用链表存储栈中的元素。栈中元素的插入和删除仅在栈顶进行,因此不必设置头节点,链表的头指针就是栈顶指针。
函数调用和返回控制是用栈实现的。(19年第22题)
- **队列**
队列是按“先进先出”的规则进行操作的。 (21年第7题)
(1)**顺序队列**
用一组地址连续的存储单元依次存储队列的数据元素。由于队中元素的插入和删除限定在表的两端进行,因此设置队头指针和队尾指针。
(2)**链队列**
为了便于操作,可给链队列添加一个头节点,并令头指针指向头节点。因此,队列为空的判定条件是头指针和尾指针的值相同,且均指向头节点。
例题:
设栈 s 和队列 q
的初始状态为空,元素a、b、c、d、e依次进入栈s,当一个元素从栈中出来后立即进入队列q。若从队列的输出端依次得到元素c、d、b、a、e,则栈s的容量至少为()
解:看栈最多的时候能容纳多少元素。

字符串是一串文字及符号的简称,是一种特殊的线性表。
字符串的基本数据元素是字符,常常把一个串作为一个整体来处理。
- **串的定义及基本运算**
串是仅由字符构成的有限序列,是取值范围受限的线性表。
一般记为 S=‘a1a2…an’,其中 S 是串名,单引号括起来的字符序列是串值。
• 串长:即串的长度,指字符串中的字符个数。
• 空串:长度为0的空串,空串不包含任何字符。
• 空格串:由一个或多个空格组成的串。
• 子串:由串中任意长度的连续字符构成的序列称为子串。
• 串相等:指两个串长度相等且对应位置上的字符也相同。
• 串比较:两个串比较大小时以字符的ASCII码值作为依据。
- **串的存储结构**
(1)**顺序存储** :用一组地址连续的存储单元来存储串值的字符序列

(2)**链式存储** :字符串可以采用链表作为存储结构,当用链表存储串 中的字符时,每个结点中可以存储一个字符,也可以存储多个字符。

- **字符串运算**
- **串的模式比较**
3.2 数组和矩阵 87
- **数组**
一维数组是长度固定的线性表,数组中的每个数据元素类型相同。n维数组是定长 线性表在维数上的扩张,即线性表中的元素又是一个线性表。
由于数组一般不做插入和删除,且元素个数和元素之间的关系不再发生变动,那 么数组适合采用顺序存储结构。
二维数组的存储结构可分为以行为主序(按行存储)和以列为主序 (按列存储)两种方法。
设每个数据元素占用L个单元,m、n为数组的行数和列数,那么:
以行为主序优先存储的地址计算公式为: Loc(aij)=Loc(a11)+((i-1)×n+(j-1))×L
以列为主序优先存储的地址计算公式为: Loc(aij)=Loc(a11)+((j-1)×m+(i-1))×L
- **矩阵**
• 这里主要讨论一些特殊矩阵的压缩存储的问题。
• 对多个值相同的元素可以只分配一个存储单元,零元素不分配存储单 元。
• 下面主要讨论对称矩阵、三对角矩阵、稀疏矩阵。
(1)对称矩阵
若矩阵An×n中的元素有aij=aji(1≤i,j≤n)的特点,则称之为对称矩阵。 如:
• 则矩阵An×n的n2个元素可以压缩存储到可以存放n(n+1)/2个元素的存储 空间中。 • 假设以行为主序存储下三角(包括对角线)中的元素,并以一个一维
数组B[n(n+1)/2]作为n阶对称矩阵A中元素的存储空间,则B[k] (0≤k<n(n+1)/2)与矩阵元素aij(aji)之间存在着一一对应的关系:
(2)三对角矩阵
• 对角矩阵是指矩阵中的非零元素都集中在以主对角线为中心的带状区 域中,其余的矩阵元素都为零。
• 下面主要考虑三对角矩阵,即只有主对角线及其左右两边为非零元素。
• 若以行为主序将n阶三对角矩阵An×n的非零元素存储在一维数组B[k] (0≤k<3n-2)中,则元素位置之间的对应关系为: k=3 ×
(i-1)-1+j-i+1=2i+j-3 (1≤i,j≤n)
• 在一个矩阵中,若非零元素的个数远远少于零元素的个数,且非零元 素的分布没有规律,则称之为稀疏矩阵。
• 可以用一个三元组(i,j,aij)唯一确定矩阵中的一个元素。
3.3 树和图 90
- **树的定义**
树是n(n≥0)个结点的有限集合。当n=0时称为空树。在任一非空树中,有且仅有一个称为根的结点;其余结点可分为m(m≥0)个互不相交的有限集T1,T2…,Tm,其中每个集合又都是一棵树,并且称为根结点的子树。
(1)双亲、孩子和兄弟
(2)结点的度:一个结点的子树的个数记为该结点的度。
(3)叶子结点:也称为终端结点,指度为零的结点。
(4)内部结点:度不为零的结点称为分支结点或非终端结点。除根结点之外,分支 结点也称为内部结点。
(5)结点的层次:根为第一层,根的孩子在第二层,依此类推。
(6)树的高度:一棵树的最大层次数记为树的高度(或深度)。
(7)有序(无序)树:若将树中结点的各子树看成是从左到右具有次序的,即不能 交换,则称该树为有序树,否则称为无序树。
(8)森林:m(m≥0)棵互不相交的树的集合。
- **二叉树的定义**
定义:二叉树是n(n≥0) 个结点的有限集合,它或者是空树 (n=0),或者是由一个根结点及两棵不相交的、分别称为左子树和右子树的二叉树所组成。
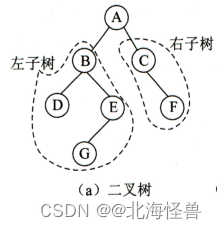
树和二叉树的区别:
(1)二叉树中结点的子树要区分左子树和右子树, 即使只有一棵子树,而树中不用区分。
(2)二叉树中结点的最大度为 2,而树中无限制。
- 二叉树的性质 (21年第8题)
性质1:二叉树第i(i≥1)层上至多有 2^(i-1) 个节点。
性质2:深度为k 的二叉树至多有 2^k-1 个结点(k≥1)。
性质3:对任何一棵二叉树,若其终端结点数为n0,度为2的结点数为n2,则 n0=n2+1
性质4:具有n个结点的完全二叉树的深度为log2n + 1
- 二叉树的存储结构


- **二叉树的遍历** (15年第21题)
遍历是按某种策略访问树中的每个结点,且仅访问一次。
依据访问根结点次序的不同,可分为前序遍历法、中序遍历法、后序遍历法。
(1)中序遍历法:(左、根、右)
① 中序遍历根的左子树。
② 访问根结点。
③ 中序遍历根的右子树。
依此类推。
(2)前序遍历法:先访问根结点(根、左、右)
(3)后序遍历法:后访问根结点(左、右,根)
(4)层序遍历法:按层从上至下、每层从左至右的顺序遍历
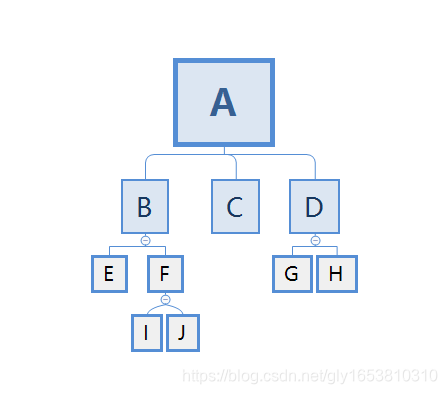
前序遍历:A B E F I J C D G H
后序遍历:E I J F B C G H D A
层次遍历:A B C D E F G H I J
- 最优二叉树
最优二叉树又称哈夫曼树,是一类带权路径长度最短的树。
• 权:是一个人为的概念,表示计算机对每个结点的访问频率。
• 路径长度:是每一个结点到根结点的路径的长度。
• 结点的带权路径长度:是指从该结点到根结点之间的路径长度与该结点权的乘积。
• 树的带权路径长度为树中所有叶子结点的带权路径长度之和。
• 构造最优二叉树的哈夫曼方法:
(1)根据给定的 n 个权值{w1,w2,…,wn}构成n棵二叉树的集合F={T1,T2,…,Tn}, 其中每棵树 Ti 只有一个带权为 wi
的根结点,其左右子树均空。
(2)在F中选取两棵根结点的权值最小的树作为左右子树,构造一棵新的二叉树, 置新构造二叉树的根结点的权值为其左、右子树根结点的权值之和。
(3)从F中删除这两棵树,同时将新得到的二叉树加入到F中。 重复(2)(3)步,直到F中只含一棵树时为止,这棵树便是最优二叉树(哈夫曼树)。
• 最优二叉树的一个应用是对字符集中的字符进行编码和译码。
- **二叉查找树 (二叉排序树)** (09年第27题)
• 它或者是一棵空树,或者是具有如下性质的二叉树:
(1)若它的左子树非空,则左子树上所有结点的关键码值均小于根结点的关键码值。
(2)若它的右子树非空,则右子树上所有结点的关键码值均大于根结点的关键码值。
(3)左、右子树本身就是两棵二叉查找树。
• 对二叉查找树进行中序遍历,可得到一个关键码递增有序的结点序列。
• 二叉查找树的作用:使用二叉查找树来查找树中的数值比普通的二叉树更为方便。
• 构造二叉树时需进行平衡华处理,使每个节点左右子树的高度的绝对值不超过1。
给定N个权值作为N个叶子结点,构造一颗二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
霍夫曼树可以用来进行通信电文的编码和解码。
(1) B-树中,所有非终端结点也就是非叶子结点都会包含关键字;
(2) 所有叶子结点都出现在同一层次上并且不带信息(可以看作是外部结点或查找失败的结点),层次相同也就是高度相同,从根结点到每个叶子结点的路径长度相同;
(3) 所有非终端结点包含的关键字数量是不确定的,指向的子树个数也是不确定的。
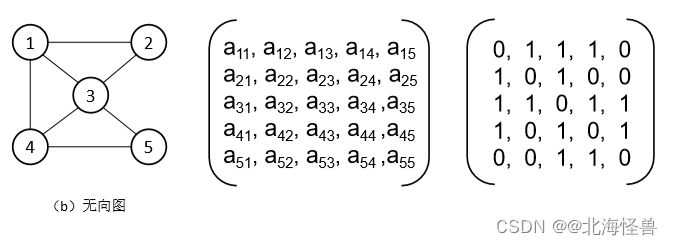
图G(Graph)是由两个集合:V和E所组成的,V是有限的非空顶点
(Vertex)集合,E是用顶点表示的边(Edge)集合,图G的顶点集和边集分别记为V(G)和E(G),而将图G记作G=(V,E)。
可以看出,一个顶点集合与连接这些顶点的边的集合可以唯一表示一个图。
在图中,数据结构中的数据元素用顶点表示,数据元素之间的关系用边表示
终点称为弧头。

有向图a的顶点集合为: V(a)={1,2,3,4}
边的集合为: E(a)={<1, 2>,<1, 3>,<4, 2>,<1, 4>,<4, 1>}

左侧无向图b的顶点集合为: V(b)={1,2,3,4,5}
边的集合为: E(b)={(1, 2),(1, 3),(1, 4),(4, 5),(2, 3),(3, 4), (3, 5)}
共有n(n-1)/2条边,类似地,有n个顶点的有向完全图中弧的数目为 n(n-1),即任意两个不同顶点之间都存在方向相反的两条弧。
顶点 v 的度是指关联于该顶点的边的数目,记作D(v)
若为有向图,度表示该顶点的入度和出度之和
顶点的入度是以该顶点为终点的有向边的数目
顶点的出度指以该顶点为起点的有向边的数目
- 图的存储结构

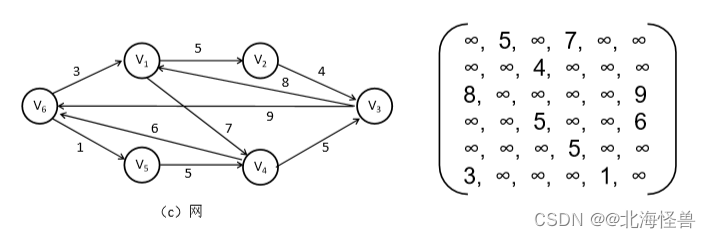
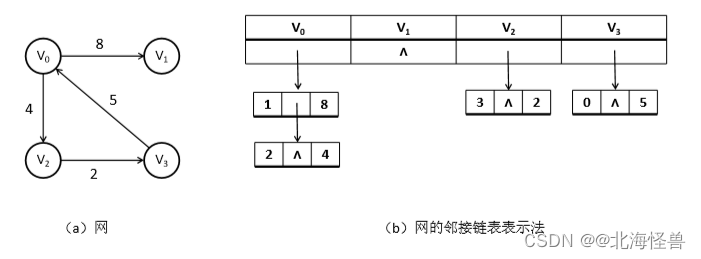
邻接链表是为图的每一个顶点建立一个单链表,第i个单链表中的节点 表示依附于顶点vi的表(对于有向图是以vi为尾的弧)。
• 邻接链表中的表节点有表节点和表头节点两种类型:
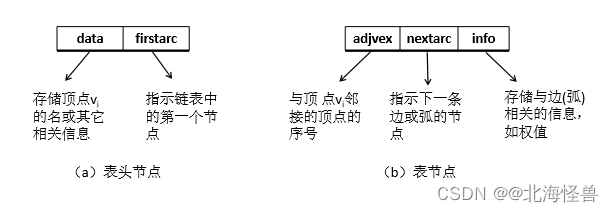
无向图的邻接链表表示法

有向图的邻接链表表示法

带权值的网的邻接链表表示法
3.4 常用算法 102
- 作者:Maynor
- 链接:https://maynor1024.live/article/2dd1f390-6aa9-8148-828c-c7911f58e517
- 声明:本文采用 CC BY-NC-SA 4.0 许可协议,转载请注明出处。
